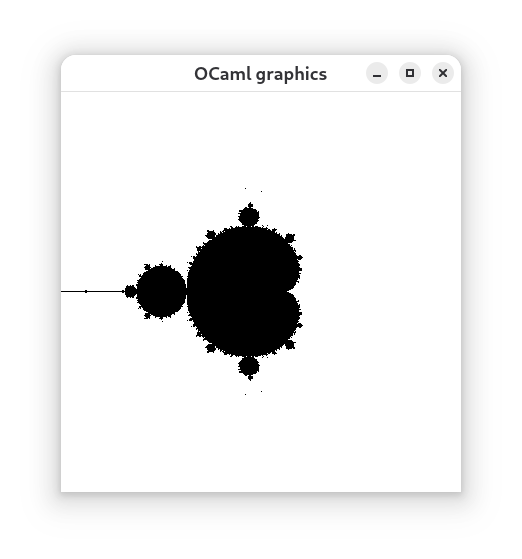
Mandelbrot Set
A solution to display the Mandelbrot Set using the OCaml programming language.
Taken from Learn Programming with OCaml.
Solution
open Graphics
let width = 800
let height = 800
let k = 100
let norm2 x y = x *. x +. y *. y
let mandelbrot a b =
let rec mandel_rec x y i =
if i = k || norm2 x y > 4. then i = k
else
let x' = x *. x -. y *. y +. a in
let y' = 2. *. x *. y +. b in
mandel_rec x' y' (i + 1)
in
mandel_rec 0. 0. 0
let draw () =
for w = 0 to width - 1 do
for h = 0 to height - 1 do
let a = 4. *. float w /. float width -. 2. in
let b = 4. *. float h /. float height -. 2. in
if mandelbrot a b then plot w h
done
done
let () =
let dim = Printf.sprintf " %dx%d" width height in
open_graph dim;
draw ();
ignore (read_key ())